Week 6(19-23 August)

Continuing our ISB course on Unsupervised Learning, we completed 2 videos this week whose topics are as follows:

Introduction to Bayesian Learning

Bayes' Theorem: Bayes’ theorem describes how the conditional probability of an event or a hypothesis can be computed using evidence and prior knowledge.
The Bayes’ theorem is given by:
P(θ|X)=P(X|θ)P(θ)P(X)

 P(θ) -
P(θ)
Prior Probability is the probability of the hypothesis 
θθ
 being true before applying the Bayes’ theorem. Prior represents the beliefs that we have gained through past experience, which refers to either common sense or an outcome of Bayes’ theorem for some past observations.


P(X|θ)P(X|θ)
 - Likelihood is the conditional probability of the evidence given a hypothesis.



P(X)P(X)
 - Evidence term denotes the probability of evidence or data.


Types of distributions: 

  • Binomial distribution
  • Bernoullie distribution
  • Mutinomial distribution
  • Poisson Distribution

Clustering

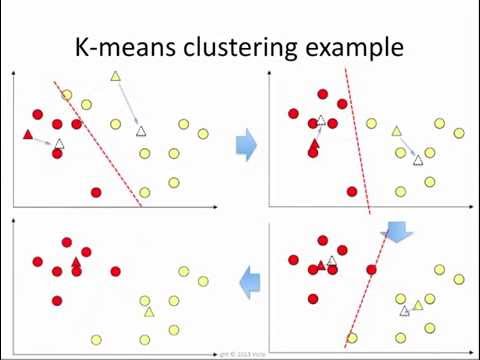
K-Means:

K-means clustering is a type of unsupervised learning, which is used when you have unlabeled data (i.e., data without defined categories or groups). The goal of this algorithm is to find groups in the data, with the number of groups represented by the variable K. The algorithm works iteratively to assign each data point to one of K groups based on the features that are provided. Data points are clustered based on feature similarity. The results of the K-means clustering algorithm are:

  1. The centroids of the K clusters, which can be used to label new data
  2. Labels for the training data (each data point is assigned to a single cluster)
    Image result for k-means clustering
Expectation Maximization:
The Expectation-Maximization (EM) algorithm is a way to find maximum-likelihood estimates for model parameters when your data is incomplete, has missing data points, or has unobserved (hidden) latent variables. It is an iterative way to approximate the maximum likelihood function. While maximum likelihood estimation can find the “best fit” model for a set of data, it doesn’t work particularly well for incomplete data sets. The more complex EM algorithm can find model parameters even if you have missing data. It works by choosing random values for the missing data points, and using those guesses to estimate a second set of data. The new values are used to create a better guess for the first set, and the process continues until the algorithm converges on a fixed point.

Session with Vikram sir

After clearing all the concepts of EDA and Feature Engineering, we practised on some datasets and then Vikram sir instructed us to find data sets individually as work on them.

After submissions before the dealine, he evaluated our performance and made us aware of our mistakes and how we can improve our skills.

It proved to be very helpful as EDA and feature engineering are an essential part of machine learning without which model cannot be trained. 

Comments

Post a Comment

Popular posts from this blog

week 13( 4-8 November)

Image
Statistics By Sehra Sir We had been having sessions with Sukhjit Sehra Sir on statistics since the past week. This week we learned about the following topics: Probability and Probability Distributions Probability theory developed from the study of games of chance like dice and cards.  A process like flipping a coin, rolling a die or drawing a card from a deck is called probability experiments.  An outcome is a specific result of a single trial of a probability experiment. Probability Distributions Probability theory is the foundation for statistical inference.  A probability distribution is a device for indicating the values that a random variable may have.  There are two categories of random variables.  These are discrete random variables and continuous random variables. Discrete random variable The probability distribution of a discrete random variable specifies all possible values of a discrete random variable along with their respective probabilities. Example
Read more

week 11(21-25 october)

Image
After completing my news article recommender last week the upcoming week brought me opportunity to explore a library for high dimensional space visualization t-SNE , I was told by my mentor Mr.Vikram Jha to explore it and tell insights. t-SNE t-Distributed Stochastic Neighbor Embedding (t-SNE) is a ( prize-winning ) technique for dimensionality reduction that is particularly well suited for the visualization of high-dimensional datasets. Before jumping to t-SNE i knew about old technique of dimensionality reduction that is PCA,  Principal Component Analysis, I first studied in ISB videos but when Sarabjot sir explained,it  became thorough PCA Principal component analysis (PCA) is a technique used to emphasize variation and bring out strong patterns in a dataset. It's often used to make data easy to explore and visualize.
Read more

week 14(11 -15 November)

Image
In this week , we continued with deep learning course lecture no.2 "The neural net as a universal approximator" which includes recap of previous lecture related to perceptron and its firing condition.After that we first learned about deep layer structures,then we move on to multilayer perceptrons and how it is used to evaluate boolean expression , learning geometrical shapes and also learnt about required optimal depth for a neural network. Another task was given to us by Sehra sir i.e. hypothesis testing and z-statistics assignment using R.There were 3-4 assignments which was supposed to be completed in 3 days. We also watched Danko sir's lecture no.2 .The lecture was about first understandig human level intelligence and how can we achieve that in computers.He taught us about electic models and specialized models also.
Read more